Teil II Zum Modellieren der Tiden aller Weltozeane
(Ausschnitt aus "Vom Satticker Bauern und Cowboy zum Mathematiker und Modellierer der naturtreuen Tiden aller Weltozeane" von Dr. rer. nat. und Dipl. math. Ernst Walter Schwiderski , veröffentlicht im Treuburger Heimatbrief Ausgabe Juni 1994, Herg. Sabine Czygan, Lübeck, Seite 49 bis 53)
Wie man in Dichtung und Musik finden kann, haben ruhelos schwellende Meereswellen mit ihren wirbelnden und schäumenden Fluten die Menschheit von Anfang an fasziniert und inspiriert. Schon vor 2000 Jahren beobachtete der griechische Begründer der Geisteswissenschaften Aristoteles (384-322 v. Chr .) Gezeitenströme von den Kliffen der Insel Negropont. Von den wilden Wirbeln verwirrt und verzweifelt warf er sich hilflos in die Fluten. Fast 500 Jahre später schrieb der römische Gelehrte Plinius der Ältere (23- 102 n. Chr.): »Nach den Vorgängen in den Himmeln folgen Flut und Ebbe, Mond und Sonne wie Donner den Blitzen« .Noch vor 400 Jahren konnte der bedeutendste italienische Wissenschaftler Galileo Galilei (1564-1642) keine Deutung für seine Beobachtungen finden und tröstete sich mit einem Hinweis auf das Schicksal von Aristoteles.
Die erste mathematische Behandlung der Gezeiten mußte noch weitere 100 Jahre auf die Physik des größten englischen Wissenschaftlers Sir Isaac Newton (1642-1727) warten. Mit seiner Gravitationstheorie gelang es ihm den mechanischen Zusammenhang zwischen Gezeiten und Mond und Sonne herzustellen (ANHANG). Sein einfaches Tidenmodell erklärte endlich die mysteriösen halbtägigen Perioden der Gezeiten, die man fast an allen Küsten beobachtet hatte. Große Sorgen bereiteten ihm jedoch die Chinasegler, die ihm von hohen ganztägigen Tiden im Golf von Tonkin erzählten. Ebenso konnte er es sich nicht erklären, warum die Spitzenhöhen der Fluten nicht direkt unter Mond und Sonne erschienen, wie es sein Modell voraussetzte. Dennoch, die Gelehrten waren von Newtons Anfangserfolg so begeistert, daß die Pariser Akademie der Wissenschaften 50 Jahre später (1738) die Welt zu einem Preisausschreiben aufrief. Obwohl sich die großen Mathematiker der Zeit (wie Euler, Mac Laurin und die Bernoullis) daran beteiligten, mußten auch sie bald erkennen, daß die dafür nötigen Kenntnisse noch lange nicht reif waren. Trotzdem, sie entwickelten ein noch heute brauchbares Modell der Erdgezeiten, die auch verblüffende Hubhöhen von fast 50 cm erreichen können. In den 300 Jahren nach Newton versuchten es die besten Wissenschaftler der Welt (wie Lord Kelvin (Thomson), Laplace, Poincaré und G. I. Taylor) immer wieder ein realistisches Tidenmodell zu entwickeln. Viele glanzvolle Fortschritte führten zu den klassischen Strömungsgleichungen der Gezeiten, aber das ersehnte Modell blieb unerreichbar.
Das starke Interesse an Ozeangezeiten blieb natürlich nicht allein auf Denker, Dichter und Sänger beschränkt. Die allgewaltigen Kräfte der Gezeitenströme haben Landmassen an den Küsten angeschwemmt und wieder weggerissen. Sie förderten und gefährdeten Land- und Hafeningenieure, Fischer und Seeleute bei ihren täglichen Arbeiten. Spezielle Pegel wurden erfunden, die die Wasserstände stündlich anzeigen und aufzeichnen. Heute hat man über 20 Millionen stündliche Messungen an über 20.000 Pegelstationen an allen Küsten der Welt registriert und ausgewertet. Die gemessenen normalen Hubhöhen zwischen Ebbe und Flut schwanken zwischen 2 und 5 m, je nach der augenblicklichen Konstellation von Erde, Mond und Sonne. Furchterregende Höhen von 12 und 22 m werden im westlichen Englischen Kanal bzw. in der Bay of Fundy, Kanada, gemessen. In der Tiefsee erreichen die Tiden Hubhöhen von 1 bis 3 m. Mit den gemessenen Daten können Wetterberichte Küstenbewohner über den stündlichen Stand der Gezeiten informieren und warnen. Z. B. werden Badegäste an der deutschen Nordseeküste, die während sechsstündiger Ebbezeiten kilometer- weit trocken liegt, ständig über den Tidenstand informiert, um gefährliche Überraschungen zu vermeiden.
Mit den schnellen Fortschritten von Wissenschaft und Technik in den letzten 50 Jahren wurde die Suche nach einem naturtreuen Modell der Ozeangezeiten zu einem dringenden Problem. Um es endgültig zu lösen, rief die IUGG in Jahre 1965 eine internationale Arbeitsgruppe von Mathematikern (wie Accad und Pekeris, Israel, Estes und Parke, U.S.A., Hansen und Zahel, Bundesrepublik Deutschland sowie Marchuk und Kagan UDSSR) zu Hilfe. Doch nach zehnjähriger Arbeit mit modernsten Computern mußte sich diese Gruppe erfolglos auflösen. Noch 1977 disqualifizierten die bekanntesten Experten die Mathematik als Werkzeug zur Lösung des Problems. Bis dahin hatte man über 4.000 veröffentlichte Schriften über Ozeantiden gezählt. Doch das beste mathematische Modell hatte z. B. den gesamten Nordpazifik auf den Kopf gestellt und sagte Ebben für beobachtete Fluten voraus und umgekehrt.
Die U. S. Raketen- und Satellitenprojekte, an denen sich die Marine maßgebend beteiligte, verlangte 1972 eine Voraussage der Tidenhöhen mit einer Genauigkeit von 10 cm jederzeit und überall in den Ozeanen der Welt. Da ich die farbenreiche Vorgeschichte nicht kannte, war es mir leicht meiner seltsamen Neugier zu folgen und das phantasievolle Modell zu suchen. Die 300jährigen Erfahrungen führten bald zu einer verfeinerten Modellformulierung. Doch nach vielen Computerstunden blieb der Nordpazifik immer noch auf dem Kopf stehen. Tägliche Verbesserungsversuche in den nächsten drei Jahren blieben erfolglos. Die erkannten Schwächen des klassischen Modells aber führten langsam zu einer grundlegenden Neuformulierung des Computerprogramms. Endlich nach insgesamt sechsjähriger Modellierzeit erschien im Frühjahr 1978 der Nordpazifik in naturgetreuer Gezeitenlage. Das erste Modell der sogenannten »halbtägigen Hauptidee des Mondes (kurz M2-Tide)« paßte sich realistisch über 2000 Meßwerten von allen Küsten und in der Tiefsee an.
Um die beobachteten Gezeiten genau zu modellieren, werden Mond und Sonne wegen ihrer elliptischen und schrägen Umlaufbahnen mathematisch durch eine Reihe von »scheinbaren« Monden und Sonnen ersetzt, die alle die Erde auf bestimmten Kreisbahnen mit bekannten Perioden umlaufen. Für die verlangte 10 cm Genauigkeit braucht man 6 Monde und 5 Sonnen mit 4 halbtägigen, 4 ganztägigen und 3 langen (14-tägig, monatlich und halbjährig) Perioden. Die Modellierung aller zugehörigen Teiltiden gelang ohne weitere Schwierigkeiten in den folgenden sechs Jahren. Danach war das langgesuchte Tidenmodell der Weltozeane nach insgesamt 12jähriger Arbeit gelungen. Die entsprechenden Daten sind in Tabellenform und auf magnetischen Bändern weltweit verbreitet
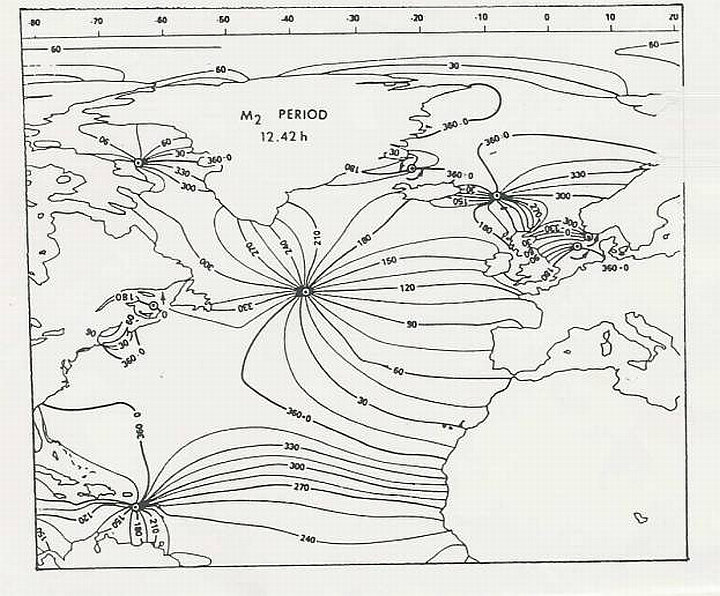
Um als Beispiel den zeitlichen Ablauf einer Periode der stark sichtbarem M2-Tide im Nordatlantik zu zeigen, sind ihre stündlichen Flutfronten in dieser Karte dargestellt.
Die wichtigsten neun Teiltiden sind in Kartenform ( »Stündlichen Flutfronten und Höhenlinien«) veranschaulicht und in » Tidenatlanten« zusammengefasst.
Wenn der Mond den Greenwich Nullmeridian passiert, liegen die Flutfronten (Hochwasserlinien auch »Cotidale Linien« genannt) entlang allen 0-Grad markierten Linien. Eine Stunde (genauer 1,035 Stunden) später liegen die Flutfronten entlang allen 30-Grad Linien, usw. Nach einer vollen M2-Periode von genau 12,52 Stunden, kehren die Flutfronten zu ihren Anfangslinien (360 = 0 Grad) zurück. Danach dreht sich eine lange M2-Flutwelle um einen Nullhöhenpunkt (»Amphidrom« genannt) südlich von Grönland und fegt im Gegenuhrzeigersinn in einem halben Tag einmal ganz über den tiefen Nordatlantik. In den flacheren Randmeeren erkennt man mehrere kleine Rotationssysteme. Z. B. hat die Nordsee zwei M2-Amphidrome: in der Mitte und an der norwegischen Südküste. Diese Rotationseigenschaft, die die M2-Tide mit allen anderen Teiltiden gemeinsam hat, hatten die Experten schon lange vorher durch die Erdrotation und die Anwesenheit der Kontinente erklärt. Unbekannt waren die naturtreue Anzahl und Lage der Amphidromien und die dazugehörigen Hubhöhen.
Die durch Küstenpegel und Tiefsee-Druckmessern bestätigte 10 cm Genauigkeit der berechneten Teiltiden wurde weiter nachgewiesen durch weltweite erfolgreiche Anwendungen in allen Disziplinen im Bereich der IUGG: Astronomie, Meteorologie, Ozeanographie, Geodäsie, Seismologie, Vulkanologie, Geophysik, und Tektonik. Z. B. konnten Experten die zeitliche Auslösung von schweren Erdbeben in Alaska, Kalifornien, China und den Philippinen mit benachbarten Ozeanfluten in Verbindung bringen. Selbst Mediziner und Psychologen glauben, daß seelische Schwankungen der Menschen durch Ozeantiden beeinflußt werden.
In Zukunft kann man erwarten, daß die Genauigkeit mit Supercomputern und mit Satellitenmessungen von 10 cm auf 1 cm verbessert werden kann. Dabei bleiben aber die hier beschriebenen Tidenkarten im wesentlichen unverändert solange Erde, Mond und Sonne ihre gegenseitigen Stellungen nicht wesentlich verändern.
(Ausschnitt aus "Vom Satticker Bauern und Cowboy zum Mathematiker und Modellierer der naturtreuen Tiden aller Weltozeane" von Dr. rer. nat. und Dipl. math. Ernst Walter Schwiderski , veröffentlicht im Treuburger Heimatbrief Ausgabe Juni 1994, Herg. Sabine Czygan, Lübeck, Seite 49 bis 53)
-----------------------------------------------------------------------------------------------------------------------
Anhang:
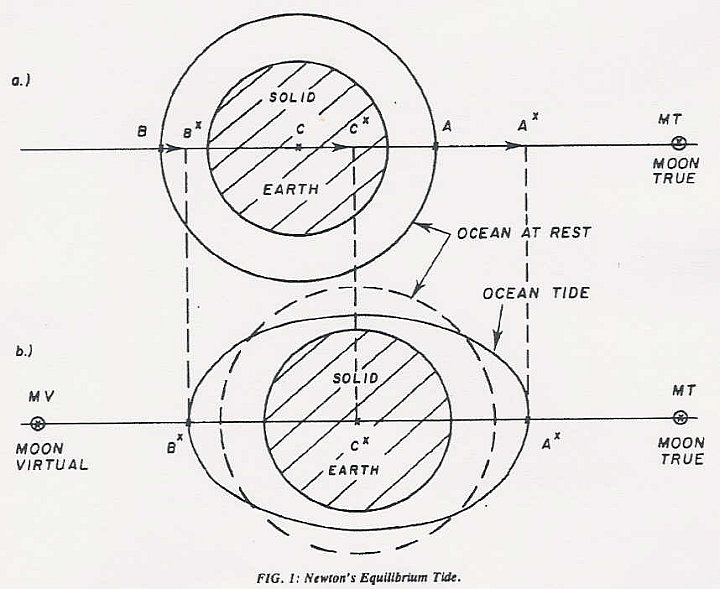
In Newton´s Modell, der Gleichgewichts Tide (Fig. 1a) zieht der wahre Mond (MT) den nächsten Ozean Punkt direkt von A nach A* an. Da die Gravitations-Kraft mit Entfernung abnimmt, wird der entfernteste Punkt etwas weniger von B nach B* angezogen. Die solide Kugel-Erde verschiebt sich als Ganzes, so daß die Erd-Mitte C in der Mitte C* zwischen A* und B* erscheint. Danach ergibt sich die Gleichgewichts Tide in der Fig. 1b. Sie zeigt zwei tägliche Höhen A* und B* scheinbar angezogen von einem wahren (MT) und einem virtuellen (MV) Mond.